円順列・数珠順列を分かりやすく解説します!!【中学生数学】

今回は数学Aで扱われる円順列とじゅず順列について解説します。公式はありますが、忘れてしまった時のために、確認しておいて下さい。
横一列に並べる場合
1~4の数字が書かれたカードを横一列に並べる場合の数
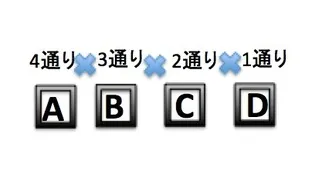
これは馴染み深い問題ですね。よくある解説ですが、A,B,C,Dの4つの座席を事前に設けておいて、その座席に1,2,3,4の数を左から順に入れます。
Aの座席には4通り、Bの座席はAにひとつ数を入れてしまったので残りの3通り、Cの座席は同様に2通り、Dは1通りになります。
4×3×2×1=4!通りが答えになります。
n個の順列は一般的にn!通りになります。
円順列
1~4の数字が書かれたカードを円形の卓に並べる場合の数
n個の円順列は(n-1)!通りですが、なぜ(n-1)通りになるのかを確認しておきましょう。
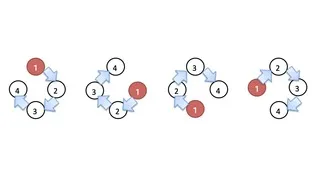
横一列の順列の場合と同様に、円卓の4つの座席をA,B,C,Dと区別し、1,2,3,4の数字を座席に入れます。

しかしながら、円順列は
「1がAに入る場合」「1がBに入る場合」「1がCに入る場合」「1がDに入る場合」
の4通りを"同じ物(1通り)"として扱います。
よって、横一列に並べる時の場合の数「4!通り」を4で割ったものが答えになります。
一般的には(n-1)!通りになります。
別の解法
1を座席Aに固定して考える方法もあります。こちらの方がメジャーな解法ですね。
固定した場合は、残りの2,3,4を座席B,C,Dに並べる順列になるので、3×2×1=3!通りになります。
じゅず順列
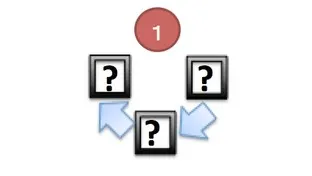
1~4の数字が書かれた球でじゅずを作る場合の数
n個のじゅず順列の公式は(n-1)!/2通りです。先ほどの、円順列の公式を2で割ったものが答えになりますが、なぜ2で割る必要があるか確認します。
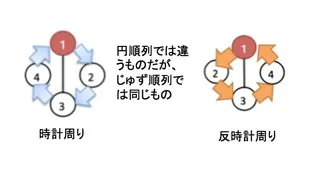
円順列の場合は、時計周り、反時計周りを区別して考えていました。
じゅず順列は、「円順列の考え方」+「時計周り、反時計回り区別しない」
そのために、円順列の場合の数の公式を2で割ります。
別の解法
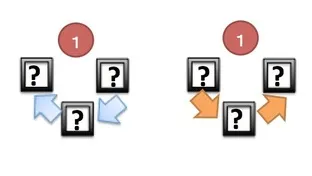
円順列の場合と同様ですが、1を座席Aに固定して考えます。「2→3→4」と「4→3→2」を同じものとして数えます。
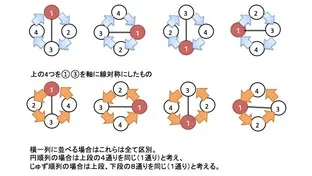
まとめ
算数・数学の人気記事
他の数学や他教科の解説記事は情報局TOPから!