たった6つの公式から三角関数の公式を全て導く方法！
たった6つの公式から三角関数の公式を全て導く方法！
三角関数の一つの壁は種々の公式を覚えなければならないことにあります。しかし、覚えるべき公式はせいぜい4つで、あとの公式はこの4つから導出できます。
↓お近くの急募塾講師バイトを今すぐ探す!↓
【東京都×急募】・【埼玉県×急募】・【神奈川県×急募】・【千葉県×急募】
覚えるべき公式は加法定理と三角関数の基本性質のみ
まずは種々の公式を導出するために最低限必要な公式を6つだけ紹介します！それが加法定理と三角関数の相互関係です。
加法定理
三角関数の相互関係
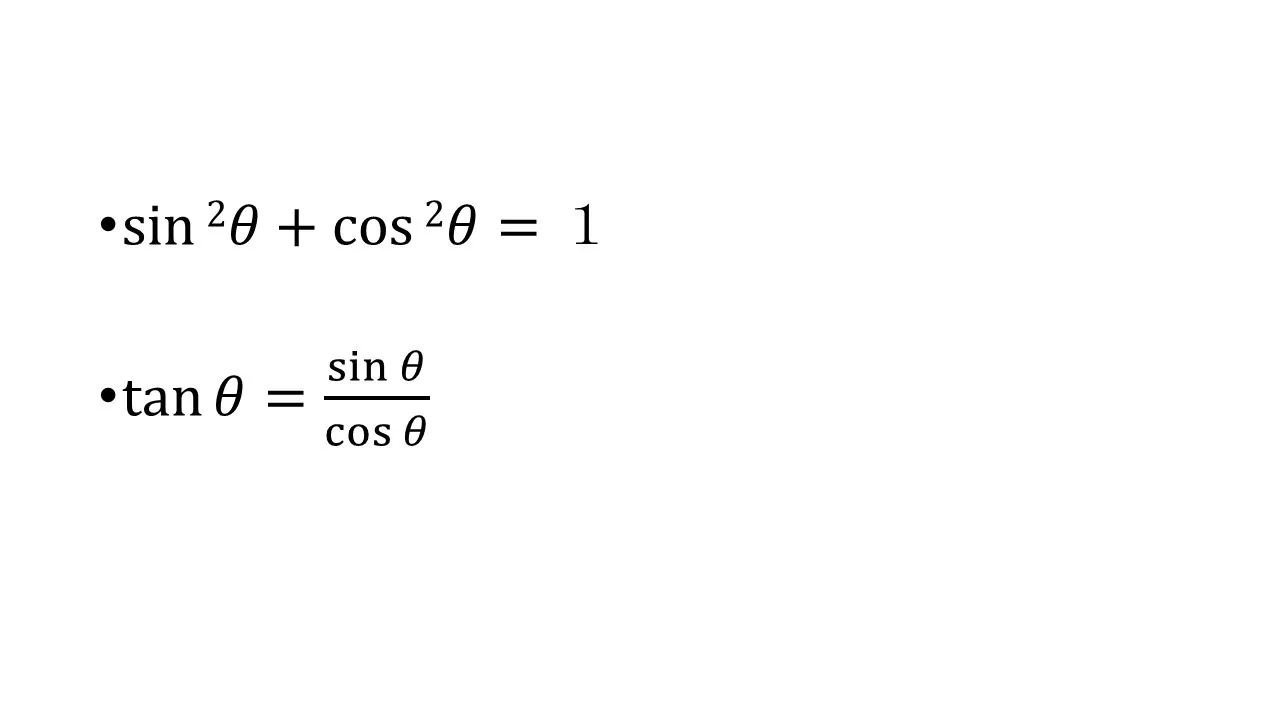
その他の公式の導出（基本編）
cos と tan の相互関係
厳密にはcosθ＝０の場合も調べなければなりませんが、上の等式はこの時も成立します。
タンジェントの加法定理
角度がマイナスのとき
＜指導の際にはこちらの方がベター＞
下の図より上記の等式は成り立つ。
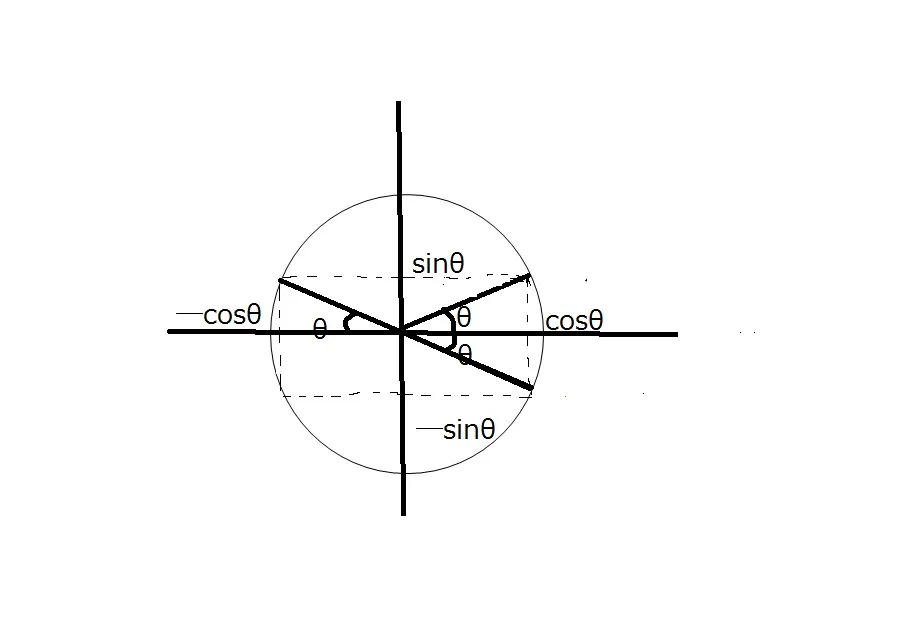
タンジェントの場合
90度の増加角
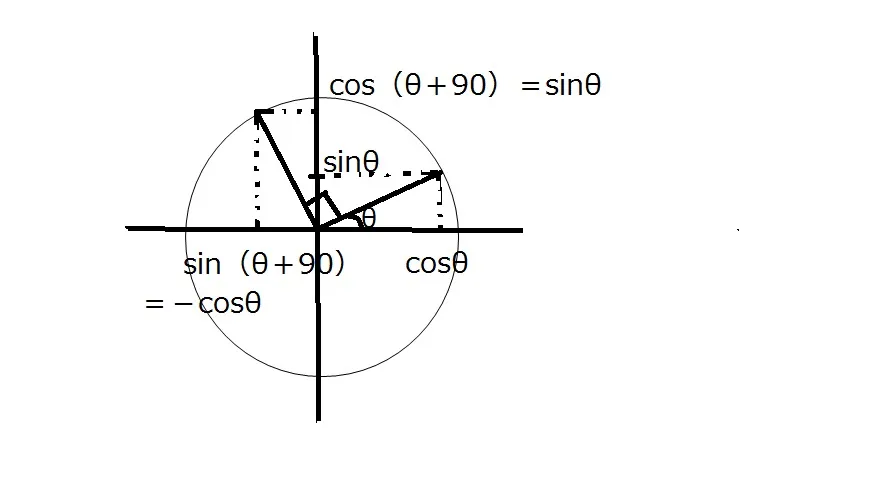＜上記の図から＞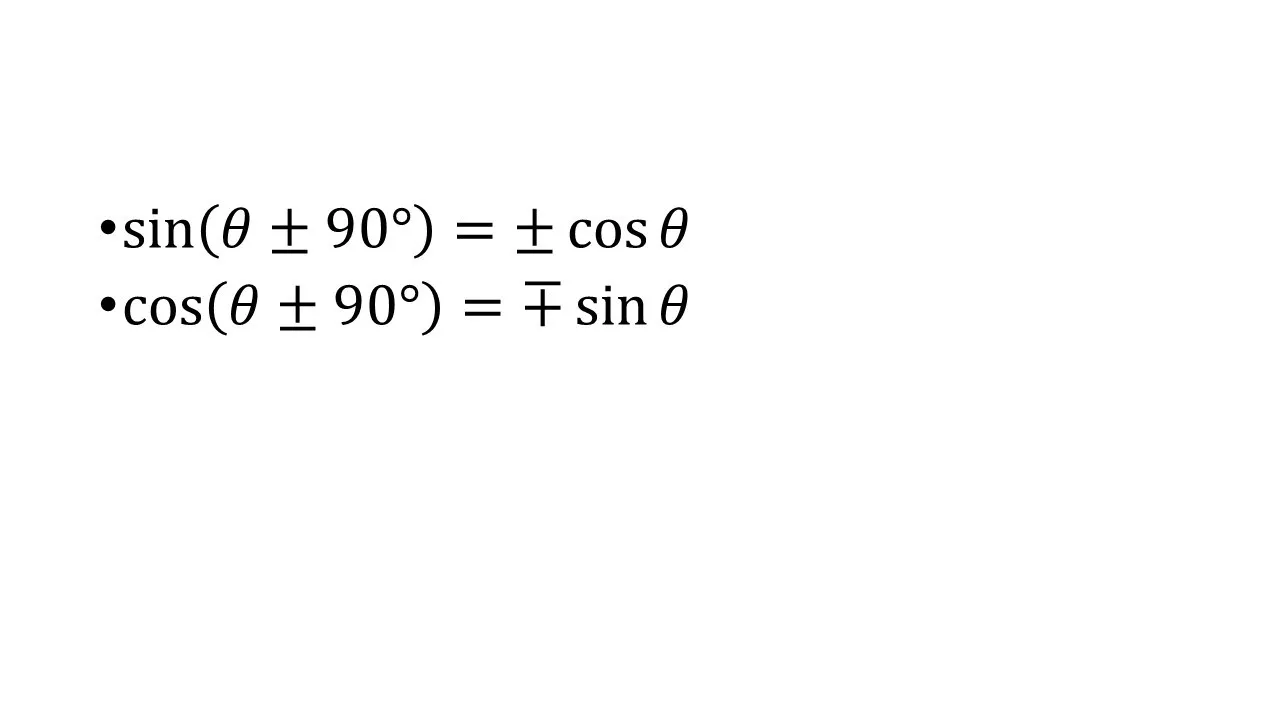
タンジェントの場合は？
これは前述のように自分で証明してみてください。とはいえ、tanθの定義に戻れば、上のsin,cosを使うだけで終了しちゃいますね。
倍角の公式
半角の公式
三倍角の公式
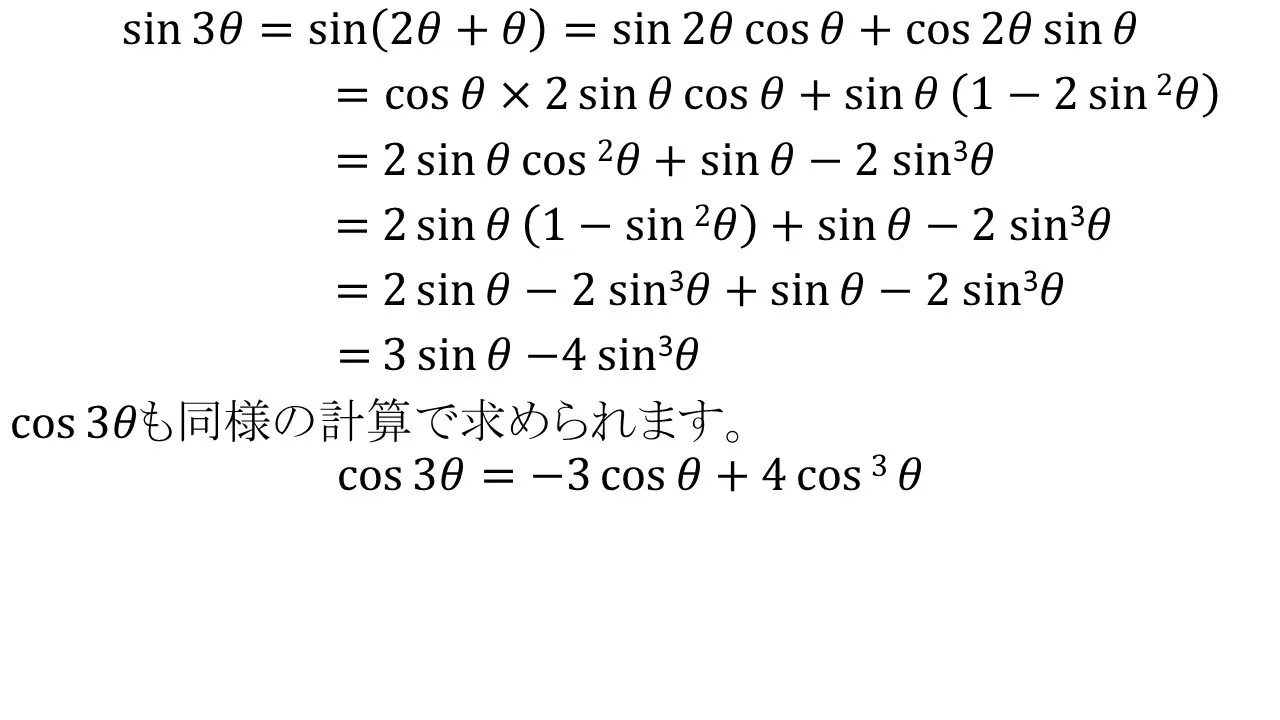
ここから下は「三角関数の和積公式」の覚え方になりますが、加法定理さえ覚えていれば十分です！冒頭でも紹介しましたがもう一度再掲します。
その他の公式の導出（和積編）
加法定理（再掲！）
でした！これを用いて下の公式を導出していきます。
積和の変換公式
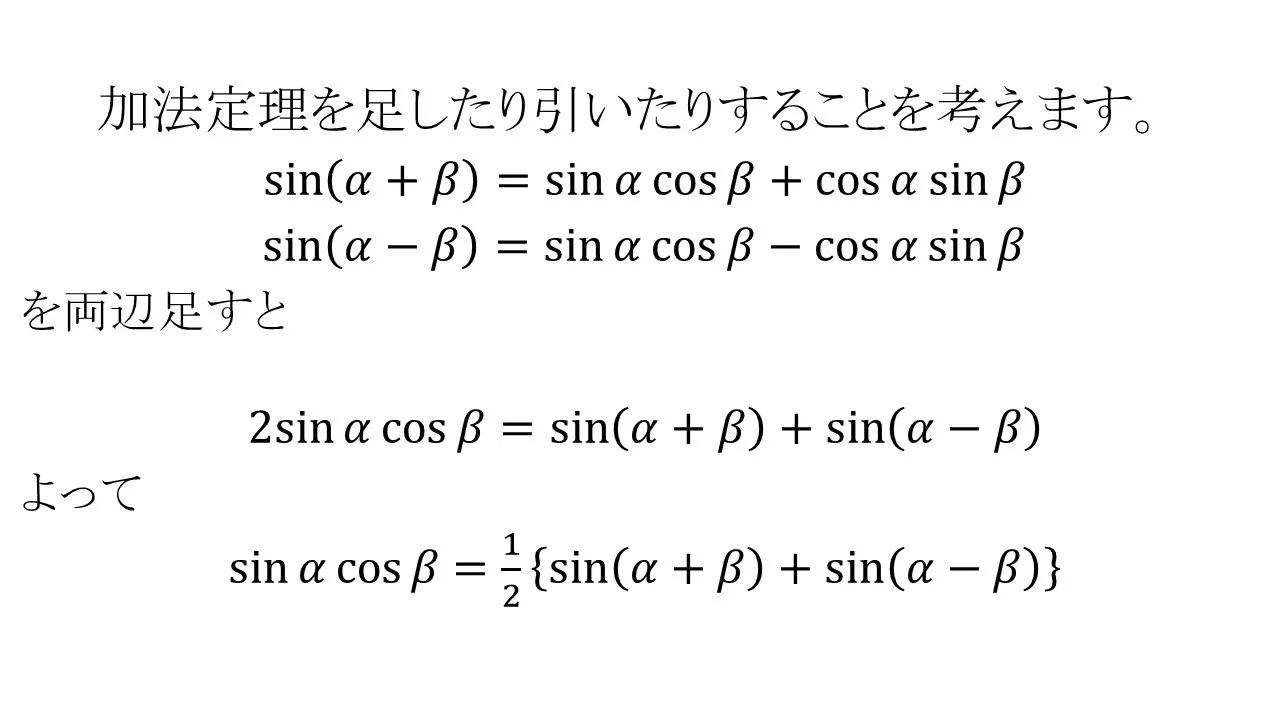
このように、加法定理の組み合わせと符号を考えて足し引きを行えば、以下の4つの積和の変換公式を導くことができます。
和積の変換公式
次に、この公式を導くためにどうすればいいか考えましょう。sinAもcosAもこのままでは加法定理を使えませんね。ならば使えるように式変形をしてあげればよいのです。なかなか思いつかないテクニカルな式変形ですが、
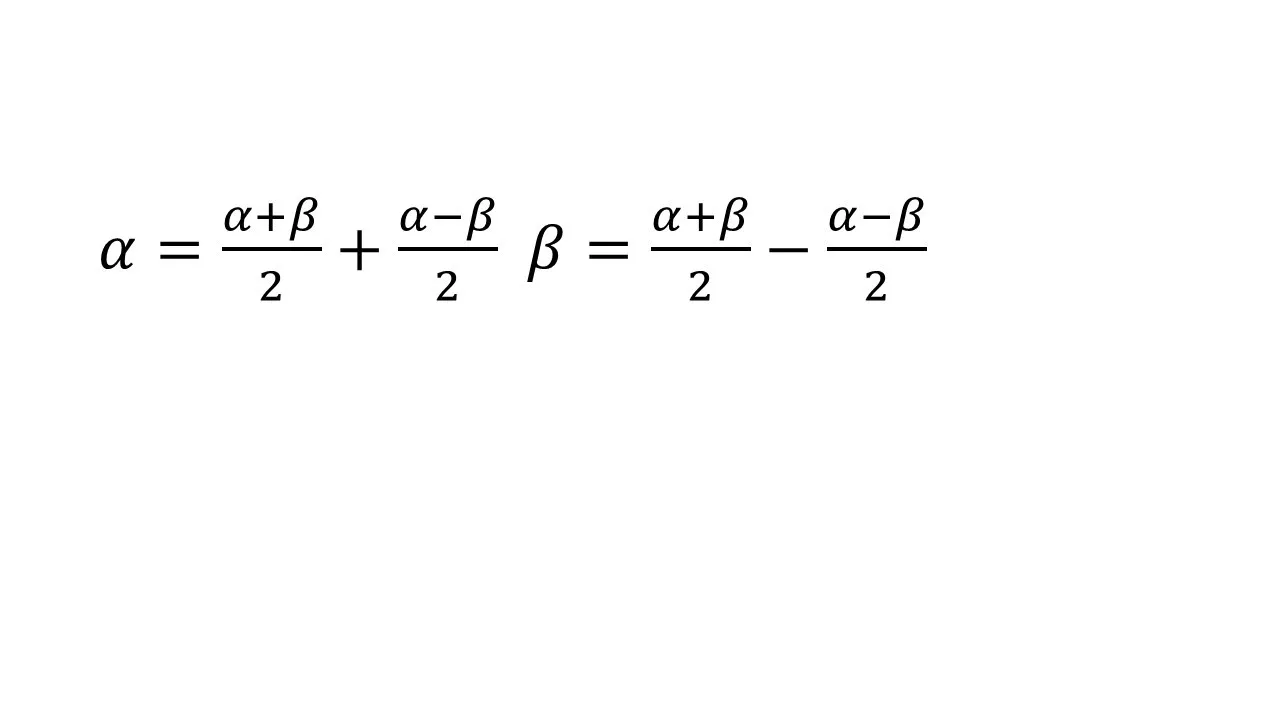
としてしまえば、加法定理を使えるので
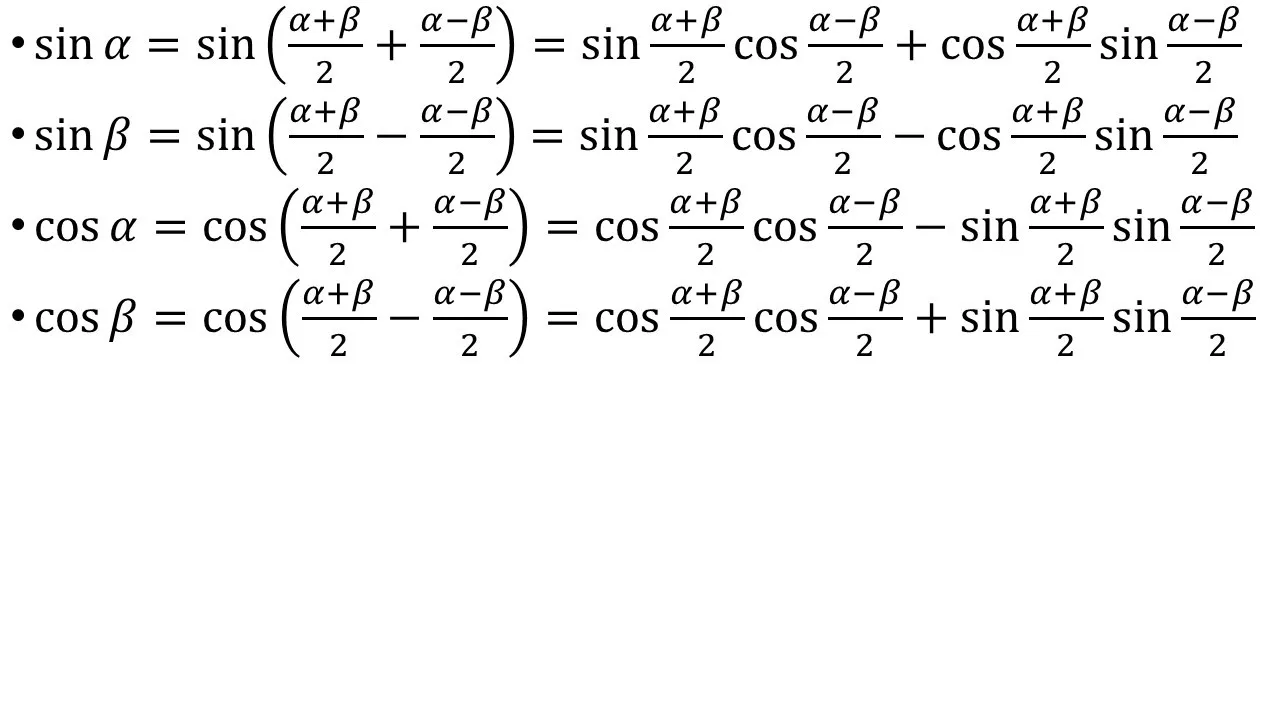
とすることができ、ここから和積の変換公式を導けます。
このように、三角関数の公式はほとんど、加法定理から導出できます。問題を解く上では覚えるに越したことはありませんが、和積の公式など出る頻度が少ないものに関しては、無理に覚えなくてもいいでしょう。
↓お近くの急募塾講師バイトを今すぐ探す!↓
【東京都×急募】・【埼玉県×急募】・【神奈川県×急募】・【千葉県×急募】
運営部おすすめ記事
![10円玉をピカピカにしよう！！[高校化学]](https://www.juku.st/cdn/article_images/304/large_juku_entry_images_image.webp)
